2022 Review 5

This was given as the final exam in Spring 2022.

Instructions

Right away - save with your name in the title.

You may consult the Picturing Programs book and the Racket Help Desk. You can even consult the presentation explaining for. Using the posn utilities, either yours or mine, is fine. You may not use any of your own work written earlier. You may not use work written by another student.

(Timing: about 90 minutes to do the animation alone.)

Short Answer

1. num-list: Integer -> (Listof Integer). Using for/list, create a list of numbers from 1 up to and including the given number.

    (check-expect (num-list 5) (list 1 2 3 4 5))
   

2. keep-multiples: Integer(m) (Listof Integer) -> (Listof Integer). Output all of the numbers in the list (the second input) that are multiples of the first number.

    (check-expect (keep-multiples 7 (list 2 14 22 7 35))
                  (list 14 7 35))
   

3. proper-divisors: Integer(m) -> (Listof Integer). Given a positive integer m, produce a list of all numbers between 1 and m (not including 1 or m) that divide m.

    (check-expect (proper-divisors 12) (list 2 3 4 6))
    (check-expect (proper-divisors 3) (list))
   

4. bishop: Integer(x) Integer(y) -> (Listof Posn). Suppose you have a bishop at coordinates (x,y) on an otherwise empty chess board. What squares can the bishop move to? The bishop moves on diagonals to the end of the board.

   We will number the squares starting at (0,0) in the lower left.

   The order that you list the posns does not matter.

    (check-expect
       (bishop 2 3)
       (list (make-posn 0 5) (make-posn 1 4) ;; (make-posn 2 3)
             (make-posn 3 2) (make-posn 4 1) (make-posn 5 0)
             (make-posn 1 2) (make-posn 0 1) (make-posn 3 4)
             (make-posn 4 5) (make-posn 5 6) (make-posn 6 7)))
   

Animation

We are going to make a number grid with some mathy features. See the video.

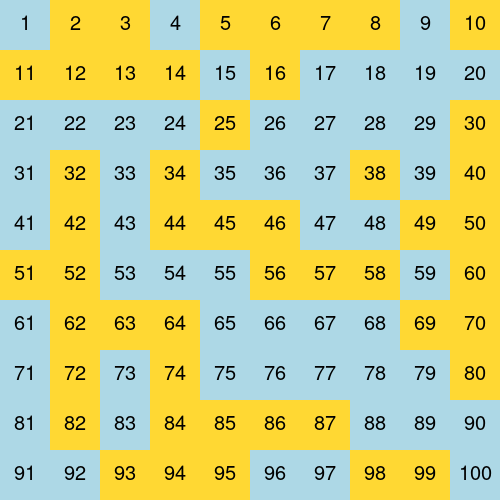
Features

1. The code has constants for width and height of the number grid. Shown above is an image using 10 for both width and height.
2. Clicking on a number flips the colors of all multiples of that number.
3. Hitting “c” clears all of the numbers (resets them back to their original color).
4. All of the prime numbers flip when the “p” key is hit. Notes: (a) this should work regardless of the size of the grid used; (b) hitting “p” twice should return the board to the state it was before you hit “p” at all.
5. The “r” key begins a time-based animation that simulates clicking on all of the numbers 1, 2, 3, etc. in succession. Mine looks good with a 0.3 second delay between each simulated click.

Starter Code

I recommend using the Locker structure with

• state is a list of numbers. A positive number k in the list means that square k is light orange. A negative number k in the list means that square k is light blue.
• next is a number. The number is the next one for the simulated click.

(require picturing-programs)
(require racket/base)
(define-struct locker (state next) #:transparent)
(define SIZE 50) ;; side length of one square
(define WIDTH 10)
(define HEIGHT 8)
(define (computer->grid p)
  (make-posn (quotient (posn-x p) SIZE)
             (quotient (posn-y p) SIZE)))
(define (grid->computer p)
  (make-posn (* SIZE (+ 1/2 (posn-x p)))
             (* SIZE (+ 1/2 (posn-y p)))))

Suggested functions:

• render-one-locker: number(k) -> image: Draw a single square in the correct color with the number on it.