2024 Review 2
You may always use helper functions. No need to ask.
There is a starter code file that contains all of the questions and checks from this page.
You may consult the Racket Help Desk,
the book Picturing Programs, and the
class web site. You may use the
posn-util without comment.
No other reference materials are allowed. (No old assignments, stack overflow, ChatGPT, etc.)
Fifteen
The Fifteen Puzzle is a solitaire game. You can play it online: github version or fancy version.

We will make this game. The play mechanic will be that you click in one spot to select a tile and then click in another spot to swap the two locations (if the move is legal). This mechanic is intended to make the game slightly easier to write.
In order for a move to be legal, one of the two clicks has to be on the empty square.
The ft structure will represent a tile. The p field is the
position of the tile (in grid coordinates; (1,1) is the upper left),
and the n field is the number at that position. The number 0 will
represent the empty tile.
(define-struct ft (p n))
we will also use a move structure which holds the two positions
being swapped.
(define-struct move (a b))
The game structure will contain:
ft-list: a list offtstructureslast: a posn, the last square clicked onhist: a list ofmovestructures
At first you should only worry about the ft-list.
(define-struct g (ft-list last hist))
Some variables and starter code.
(define INVALID (make-posn -1 -1))
(define WIDTH 4)
(define HEIGHT 4)
(define SIZE 50)
(define (computer->grid p)
(make-posn (add1 (quotient (posn-x p) SIZE))
(add1 (quotient (posn-y p) SIZE))))
(define (grid->computer p)
(make-posn (* SIZE (+ -1/2 (posn-x p)))
(* SIZE (+ -1/2 (posn-y p)))))
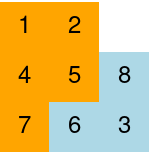
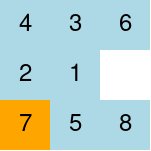
There are two 3x3 starter boards called STARTER-1 and STARTER-2. The sample board
code is in separate file.
|
|
Questions
-
(
ft-n-str) The string you should print out for the number on the square. When the number is 0, return the empty string.;; ft-n-str : Ft -> String (define (ft-n-str w) "wrong") (check-expect (ft-n-str (make-ft (make-posn 3 4) 5)) "5") (check-expect (ft-n-str (make-ft (make-posn 2 3) 0)) "") -
(
correct-location) Thecorrect-locationfunction takes in a number and puts out theposnthat the number should be in when the puzzle is solved.For credit on this problem you must use some kind of math or recursion. For full credit your method must be easily adaptable to a different sized board.
;; correct-location : Number -> Posn (define (correct-location n) INVALID) (check-expect (correct-location 1) (make-posn 1 1)) (check-expect (correct-location 2) (make-posn 2 1)) (check-expect (correct-location 4) (make-posn 4 1)) (check-expect (correct-location 5) (make-posn 1 2)) (check-expect (correct-location 15) (make-posn 3 4)) (check-expect (correct-location 0) (make-posn 4 4)) -
(
ft-color) The background of a square should be white if the number n is 0, orange if the tile is in the correct position (based on its number), and blue otherwise.;; ft-color : Ft -> String (Color) (define (ft-color w) "gray") (check-expect (ft-color (make-ft (make-posn 2 3) 0)) "white") (check-expect (ft-color (make-ft (make-posn 4 1) 4)) "orange") (check-expect (ft-color (make-ft (make-posn 3 1) 2)) "light blue") -
(
ft-draw-one) Draw a single tile on the given background. Use the color and string from above.;; ft-draw-one : Ft Image -> Image (define (ft-draw-one w bg) bg)Examples are below.
(define fig4a (draw-one (make-ft (make-posn 4 1) 4) (rectangle 200 200 "solid" "pink"))) (define fig4b (draw-one (make-ft (make-posn 2 3) 5) (empty-scene 200 200)))
Figure 4a
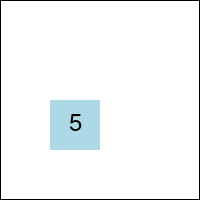
Figure 4b
-
(
ft-draw-all) Draw a list of tiles on the given background.;; ft-draw-all : (Listof Ft) Image -> Image (define (ft-draw-all ws bg) bg)An example is below.
(draw-all (list (make-ft (make-posn 4 1) 4) (make-ft (make-posn 2 3) 5)) (rectangle 200 200 "solid" "light green"))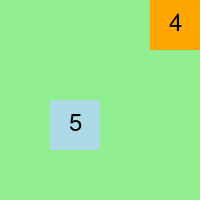
-
(
make-correct) Make a list withftstructures representing the numbers from 0 through n in their correct final locations.Write one more check-expect as well as the code.
;; make-correct : Number -> (Listof Ft) (define (make-correct n) empty) ;; for a 4x4 board (check-expect (make-correct 0) (list (make-ft (make-posn 4 4) 0))) (check-expect (make-correct 1) (list (make-ft (make-posn 1 1) 1) (make-ft (make-posn 4 4) 0))) -
(
get-num) Given a list of Ft and a Posn, return the number at that posn. Give -1 if that posn is not in the list.;; get-num : (Listof Ft) Posn -> Number (define (get-num ft-list p) -1) -
(
legal-swap?) Given a list of Ft representing the tiles on the board along with two posns, return true if it is legal to swap the tiles at those positions.A swap is legal when:
- both posns are actually on the board;
- the posns are next to each other on the board; and
- one of the numbers is zero.
Include check-expects demonstrating that all of the conditions hold. You could use the
STARTER-1-FT-LISTvariable from the starter boards.(define (legal-swap? ft-list p q) false) -
(
do-swap) Given the same information as in the previous problem, actually perform the swap that changes the positions of the two tiles. This function is not concerned whether or not the swap is actually legal. The order of terms in the result does not matter.;; do-swap : (Listof Ft) Posn Posn -> (Listof Ft) (define (do-swap ft-list p q) ft-list)Since the order of the result does not matter, these checks just make sure the values that should move are in the correct places.
(define SWAPCHECK-1 (do-swap STARTER-1-FT-LIST (make-posn 3 1) (make-posn 3 2))) (check-expect (get-num SWAPCHECK-1 (make-posn 3 1)) 8) (check-expect (get-num SWAPCHECK-1 (make-posn 3 2)) 0) (define SWAPCHECK-2 (do-swap STARTER-2-FT-LIST (make-posn 3 2) (make-posn 2 2))) (check-expect (get-num SWAPCHECK-2 (make-posn 3 2)) 1) (check-expect (get-num SWAPCHECK-2 (make-posn 2 2)) 0)
- Now you should be in a position where you can write the mouse handler and create an animation so that you can play the game.